I must admit that the BMW M4 GT3 LM surprised me in a very pleasant way. Up until now, my work on the p99 metric gave me a fairly clear picture: the Mercedes AMG GT3 LM remained reasonable with a p99 around 24.4, while the Ferrari 296 LM GT3, on the other hand, literally exploded the numbers with a value flirting with 50 Nm. That Ferrari left me with the impression that p99, as an indicator, could be misleading—because despite such huge loads, I didn’t feel the need to reduce the in-game gain as much as the calculation suggested.
Then came the BMW. I expected behavior similar to the Mercedes, but its results surprised me: depending on the track, I measured a p99 between 21 and 25, even lower than I had imagined. What’s striking is that despite this modest value, my practical LMU gain settings also end up in the same range as the Ferrari and the Mercedes: between 25 and 28. In other words, this BMW confirms my intuitions but also pushes me to go further. It shows that p99 alone is not enough to explain why, in practice, such different cars converge toward similar gain settings.

p99 results across tracks
Test conditions
All these measurements were carried out under stable and reproducible conditions: dry track, ideal temperature, and the car kept in its default setup, including original tire pressures.
For steering, I followed the “lock” value given by the game, i.e. 516° for 19.7° of lock, but I chose to round it up to 520° for a cleaner and easier-to-use value in my settings.
p99 results across track
Using MoTeC data, I extracted the p99 of the force feedback signal on several reference circuits. Here are the results obtained with the BMW M4 GT3 LM, always with the base at 12 Nm (100/100) and in-game gain set to 20:
COTA → p99 ≈ 25.2
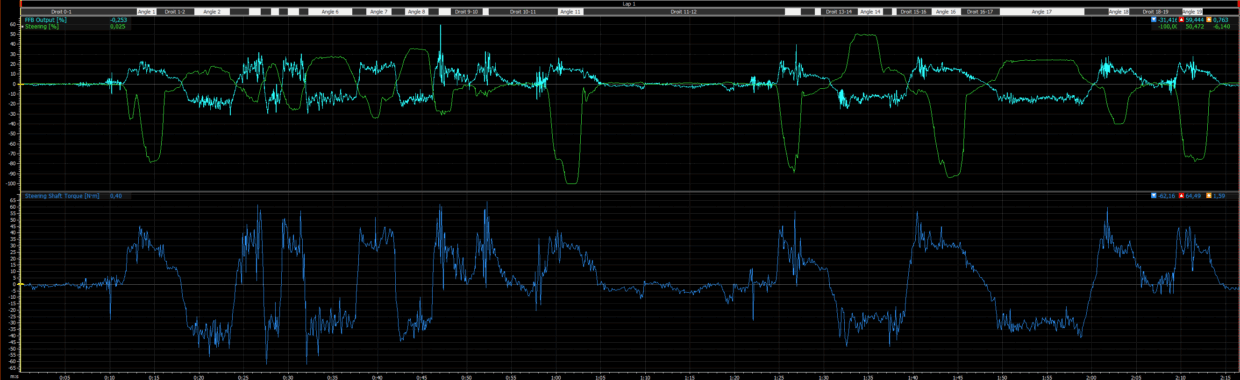
Interlagos → p99 ≈ 21.4
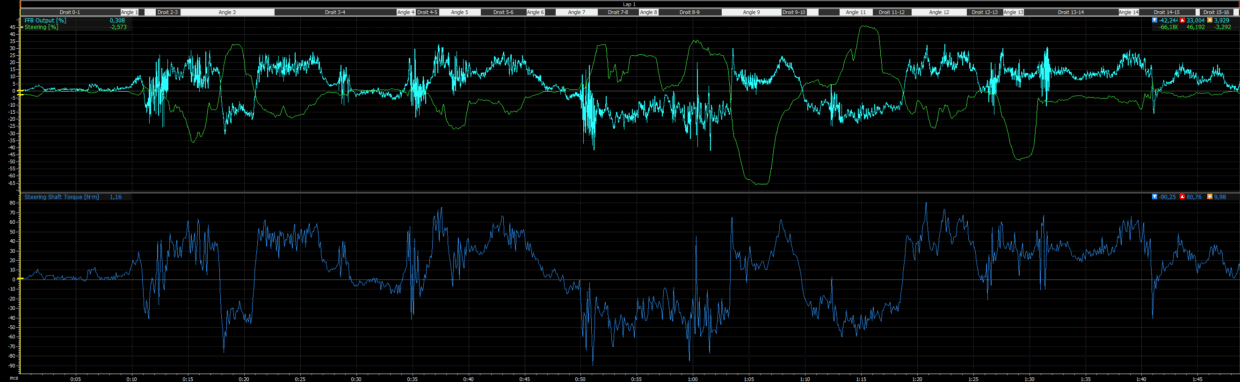
Sebring → p99 ≈ 24.4
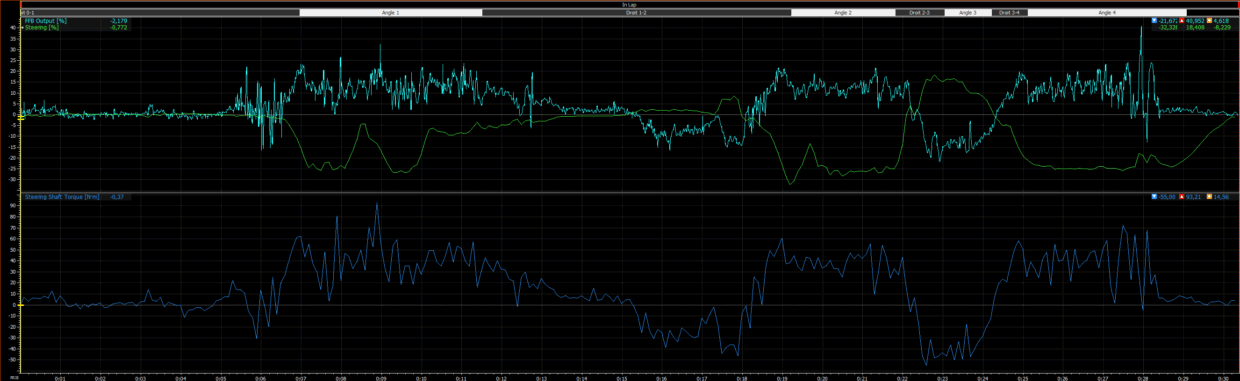
Lusail → p99 ≈ 23.4
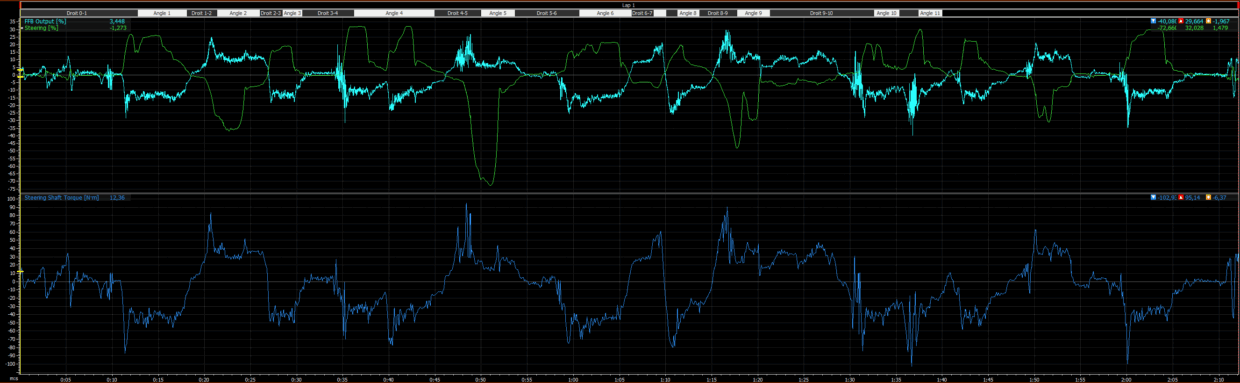
Spa-Francorchamps → p99 ≈ 24.2
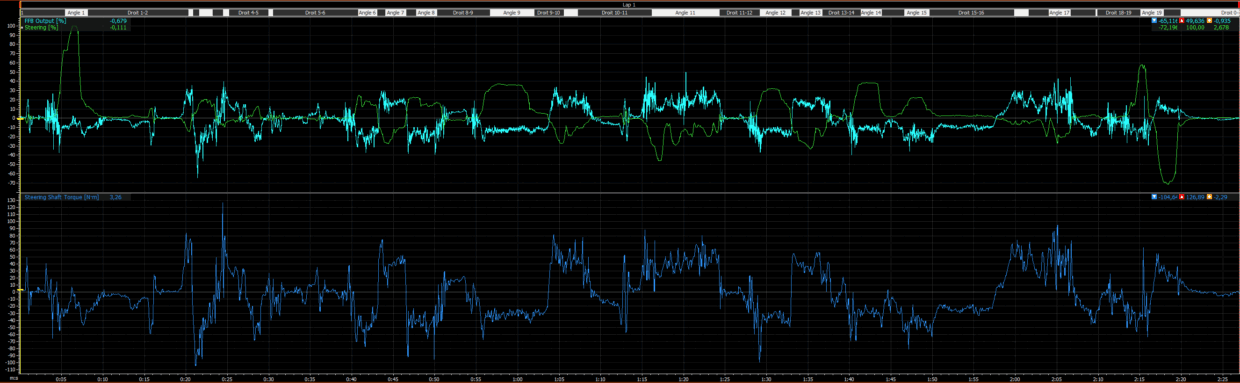
These figures confirm that the BMW remains in a homogeneous range of 22–25, with very consistent behavior across different tracks.
Numerical comparison
To better understand, I followed my usual protocol: base at 100/100 = 12 Nm, LMU gain fixed at 20, and MoTeC log analysis. Here’s what I obtained:
Mercedes AMG GT3 LM → p99 ≈ 24.4 → target gain (formula) ≈ 24
Ferrari 296 LM GT3 → p99 ≈ 50.4 → target gain (formula) ≈ 12
BMW M4 GT3 LM → p99 ≈ 21–25 → target gain (formula) ≈ 26–28
If I only looked at these numbers, I would conclude that the Ferrari should run at half the gain of the BMW. But that’s not what I feel on track. In practice, for all these cars, I always end up in the 25–28 range to achieve an expressive, balanced, and usable steering feel.

Why this paradox exists
In theory, the calculation is simple:
G new = G current x P99* / P99 current
Where p99*\star is my target (20 in my protocol).
Applying this formula, the Ferrari should logically drop to a gain of around 12, the Mercedes should be around 24, and the BMW should climb to 28. On paper, the gap is huge. But when I test these values in real conditions, the result is totally different: all three cars end up with fairly similar gains, around 25–28.
This paradox is explained by the nature of the FFB signal itself. The p99 only captures the most violent 1% of events: an aggressive curb strike, a heavy compression, or a braking phase over bumps. The Ferrari, for example, allows extreme peaks, hence its p99 of 50. But most of the time, its signal is compressed: its “everyday” values, the ones representing 90–95% of a lap, are not that far from the Mercedes or the BMW. Conversely, the BMW is much more homogeneous: its p99 is low, but its “average” load (p90, p95, RMS) ends up close to the Ferrari.
That’s when I realized that p99, taken alone, cannot be the only reference for calibrating a wheel. It’s useful for setting a limit, but it exaggerates the extremes. To build a universal protocol, I also need to consider what happens below: p90, p95, and even RMS. This combination reflects the real feeling at the wheel and explains why, despite distant p99 values, the cars end up requiring similar gains.
A method that goes beyond FFB
This work on p99 is not limited to adjusting wheel torque. In reality, it offers a much broader framework to refine my driving and my setup. Once I stabilize my gain values and know that each car falls within a coherent range, I can dedicate my attention to other critical aspects—most importantly braking.
By eliminating parasitic variations in the FFB, I noticed my braking references became much more consistent. I can feel more precisely how the load transfers to the front, the micro-rotation induced by ABS, or the gradual rear grip loss. This consistency is not trivial: it allows me to attack with more confidence, lap after lap, without “re-learning” the car’s behavior due to gain being too high or too low.
This work becomes even more valuable when combined with the P1 SIM Mistral pedal set. With its elastomer brake, progressiveness, and precision in modulation, the pedal set is the perfect complement to the p99 protocol. Together, wheel and pedals form a couple that gives me a nearly professional vision of Le Mans Ultimate.

Elastomers for the P1 SIM Mistral pedal set
To reproduce the braking characteristics of the BMW M4 GT3 LM, the choice of elastomers in the P1 SIM Mistral pedal set is critical.
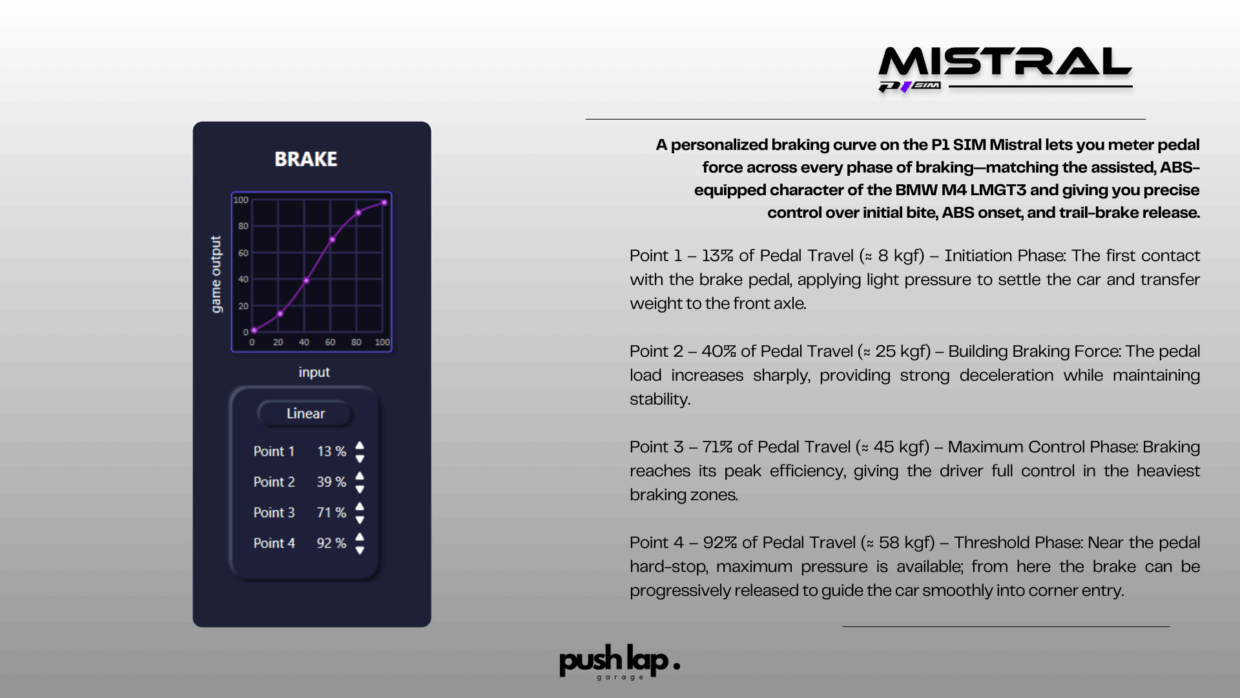
Based on our telemetry analysis (≈ 58–60 kgf peak pedal load), the optimal stack combines a soft initial element for bite, followed by progressively medium to hard compounds to replicate the firm resistance of a GT3 brake system.

This elastomer profile mirrors the BMW’s balance: sharp initial response without aggressiveness, a stable mid-phase for consistency lap after lap, and a solid limit zone that reflects the telemetry pressure plateau near ABS activation. Adjustments can be made depending on personal preference, but maintaining this progressive stiffness gradient is key to matching the physics of the M4 GT3 LM in Le Mans Ultimate.
Brake pressure (kgf)

Now that we’ve covered FFB, let’s tackle braking. To determine the ideal pressure to apply on the pedal, I looked at MoTeC telemetry where a maximum deceleration of around 2.2 g was observed. To relate this to foot effort, I rely on the P1 SIM Mistral pedal’s mechanics: a 5:1 pedal ratio and a 17.8 mm master cylinder. The piston area is therefore:
A = π x ( 17,8 / 2 ) ≈ 248 mm2 = 2.48 cm
The force applied to the piston is:
F piston = F foot / pedal ratio
and the resulting hydraulic pressure:
P = F piston / A
In practice, to achieve a deceleration of 2.2 g in a GT3, the driver must apply about 58–60 kgf at the foot.
This figure matches our observations on the BMW, placing it between the Ferrari (≈ 58 kgf) and the Mercedes (≈ 63 kgf). This range ensures both sufficient initial bite and fine modulation in the 80–90% pedal travel zone.
Brake curve (SimHub, 4 points)
The 4-point curve in SimHub transforms the mechanical pedal input (%) into a “game output” signal (%). Mathematically, each point defines a pair (x,y), where x is pedal input and y is the output sent to the simulator.
The goal is to obtain a function f(x) consistent with MoTeC data: quick efficiency rise from 10%, useful range between 40–80%, then a controlled plateau near ABS.
This ensures controlled progressiveness: sensitive from the first third, effective between 40–85%, then stabilized in a plateau near ABS. It makes the pedal highly modulable and consistent with real data.
Virtual position and MEMS sensors
For the BMW M4 GT3 LM, I chose a virtual driving position of +18 longitudinal and +4 height. This setting is not arbitrary: it aligns the driver’s visual perspective with the physical dynamics delivered by the game. If the camera is misaligned, the perceived FFB no longer perfectly matches the simulated forces, introducing a subtle but real mismatch between what you see and what you feel.
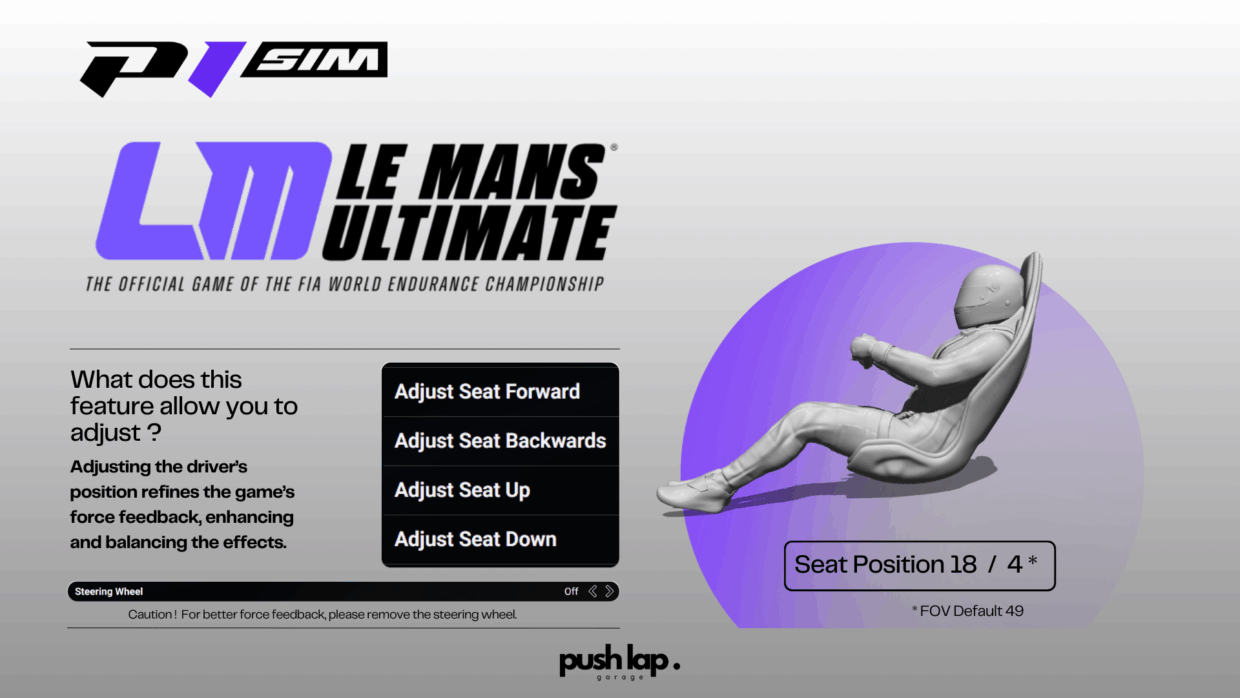
This is where the MEMS sensor analogy becomes relevant. In real cars, these micro-sensors constantly measure acceleration, vibrations, and chassis movement. The data they collect is then used by manufacturers and engineers to validate consistency between perceived and actual dynamics. In simulation, the logic should be the same: the cockpit view must align with what such sensors would “see” in a real BMW GT3. This correspondence guarantees that FFB (p99, lateral load, mass transfer) is felt exactly as intended in the car’s physical model.
In other words, the +18 / +4 driving position is far more than a visual comfort choice—it directly contributes to global fidelity by linking the camera to the underlying physics. Like MEMS in real motorsport, this subtle alignment makes the difference between simple immersion and technical credibility.
ABS settings
On the BMW M4 GT3 LM, ABS can be set from 0 to 11. Low values (1–3) minimize assistance: they promote slight oversteer on corner entry but demand very fine pedal modulation. Mid values (4–7) offer a balanced compromise between stability and agility, while high values (8–11) prioritize stability at the cost of marked understeer.

Based on MoTeC and on-track testing, the BMW works best between 5 and 6 on a dry, warm track:
ABS 5 → ideal with new tires or in cold conditions; strong bite, front grip maintained.
ABS 6 → preferable with worn tires or in hot conditions; stability preserved without losing modulation.
The key is to understand that ABS doesn’t just govern braking power—it shapes how the car rotates at entry. Low ABS allows more pivot, while high ABS locks the line but restricts aggressiveness.
Traction Control settings (TC)
TC (General sensitivity)
Determines when TC activates.
High values (8–11) → fast intervention, safer but less acceleration out of corners.
Low values (1–3) → more slip allowed, better rotation but higher risk.

TC Power Cut (Engine cut amount)
Controls how much power is removed when TC intervenes.
High values → strong cut, stable but sluggish pickup.
Low values → light cut, better drive but requires precise throttle control.

TC Slip (Slip tolerance)
Defines how much wheel slip is allowed before TC kicks in.
High values → more slip permitted, useful on abrasive tracks.
Low values → keeps the car glued down, ideal on cold or wet surfaces.

In practice, for a typical GT3 stint on dry track, a setting around TC 4–5 / Power Cut 3–4 / Slip 5–6 works well: enough freedom to exploit the BMW’s natural rotation without losing long-run consistency. These three levers should never be seen in isolation but as a dynamic balance: too much intervention and traction is muted, too little and tire wear becomes unmanageable.
My personal opinion
I must say I truly enjoy the BMW M4 GT3 LM with this FFB setup. Steering rotation set at 520°, in-game gain at 25, and my Fanatec ClubSport DD 12 Nm base kept at FOR 100% to use the full torque range, while reducing FFB to 97%(~11.6 Nm). This combination perfectly suits my driving position, “F1-style” thanks to my Playseat F1, and matches the wheel size I use.
It’s important to stress that the settings presented in this article are above all indicative references. They form a solid foundation, but each driver should fine-tune them depending on hardware and seating position. A base mounted higher or lower, different arm angles, or a more or less reclined seat—all of these affect perception of FFB and braking. These subtle details, when combined, create a unique experience. It’s precisely this sum of refinements which, when calibrated properly, delivers an exceptional level of realism and consistency in Le Mans Ultimate.
Conclusion
The BMW M4 GT3 LM study allowed us to take a new step in our methodology. Through the analysis of p99, we found that despite raw values lower than the Ferrari or Mercedes, the final FFB gain converged to the same 25–28 range. This paradox highlighted the importance of not limiting ourselves to p99, but also considering intermediate percentiles and RMS to fully understand signal consistency.
We then examined braking, linking MoTeC telemetry to actual pedal forces with the P1 SIM Mistral pedal set. The analysis showed that the BMW requires around 58–60 kgf, placing it between the Ferrari and the Mercedes. We proposed a 4-point SimHub brake curve, directly reflecting MoTeC dynamics to provide faithful modulation.
The importance of the +18 / +4 virtual position was also emphasized—not a mere visual preference, but a calibration step aligning vision and physics, exactly like MEMS sensors do in real GT3 cars.
Finally, we explored ABS and TC settings, showing that the BMW offers a wide range of combinations to adapt to driving style and track conditions. As with Ferrari and Mercedes, the balance is subtle between stability, traction, and rotation.
My personal feedback completes this study: with 520° rotation, 25 gain, and my ClubSport DD base at 97% (~11.6 Nm), the BMW M4 GT3 LM delivers a precise, consistent, and immersive force feedback.
Ultimately, this analysis confirms that realism in simulation is the sum of many small adjustments: FFB, braking, virtual position, ABS, TC, and hardware. Taken alone, each seems minor—but together, they create a coherent and professional-level experience in Le Mans Ultimate. The BMW M4 GT3 LM is a great example, once again proving that our research protocol can be successfully applied and adapted to every car.



Leave a Comment